PID Controller API Documentation
Introduction
The Aqueduct PID Controller API allows you to regulate a device's Control Output by utilizing the value of another device's Process Values. This dynamic control mechanism can be used for:
-
Backpressure Control: Use readings from a pressure transducer as the Process Value to precisely adjust a pinch valve's position as the Control Output. This may be used to control the backpressure within a Tangential Flow Filtration (TFF) system.
-
Weight-based Pump Regulation: Use weight reading from a balance as a Process Value to govern the rate of a peristaltic pump as the Control Output. This may be used to achieve or sustain a target weight, making it ideal for dosing applications.
-
Flow Rate Compensation: Use readings from a mass flow meter as the Process Value to adjust the flow rate of a peristaltic pump as the Control Output. This may be used to compensate for variations between nominal and actual flow rates.
-
pH-based Pump Regulation: Use readings from a pH probe as a Process Value to dynamically adjust the rate of a peristaltic pump as the Control Output. This maintains the desired pH level by controlling the flow of a pH-modifying solution.
Available Process Values and Control Outputs by Device Type
The examples listed above are by no means exhaustive. The API's versatility allows you to design custom control mechanisms by linking any Control Output with any available Process Value from another (or the same) device.
The following table gives an overview of the allowed Process Values and Control Outputs for different device types.
| Device Type | Allowed Process Values | Allowed Control Outputs |
|---|---|---|
| Peristaltic Pump | --- | Flow Rate |
| Syringe Pump | --- | --- |
| Solenoid Valve | --- | --- |
| Rotary Valve | --- | --- |
| Pinch Valve | --- | Position |
| Temperature Probe | Temperature | --- |
| pH Probe | pH | --- |
| Optical Density | Optical Density, Transmitted Intensity, 90° Intensity | --- |
| Mass Flow Meter | Flow Rate | --- |
| Pressure Transducer | Pressure | --- |
| Balance | Weight | --- |
Features
The Aqueduct PID Controller API offers:
-
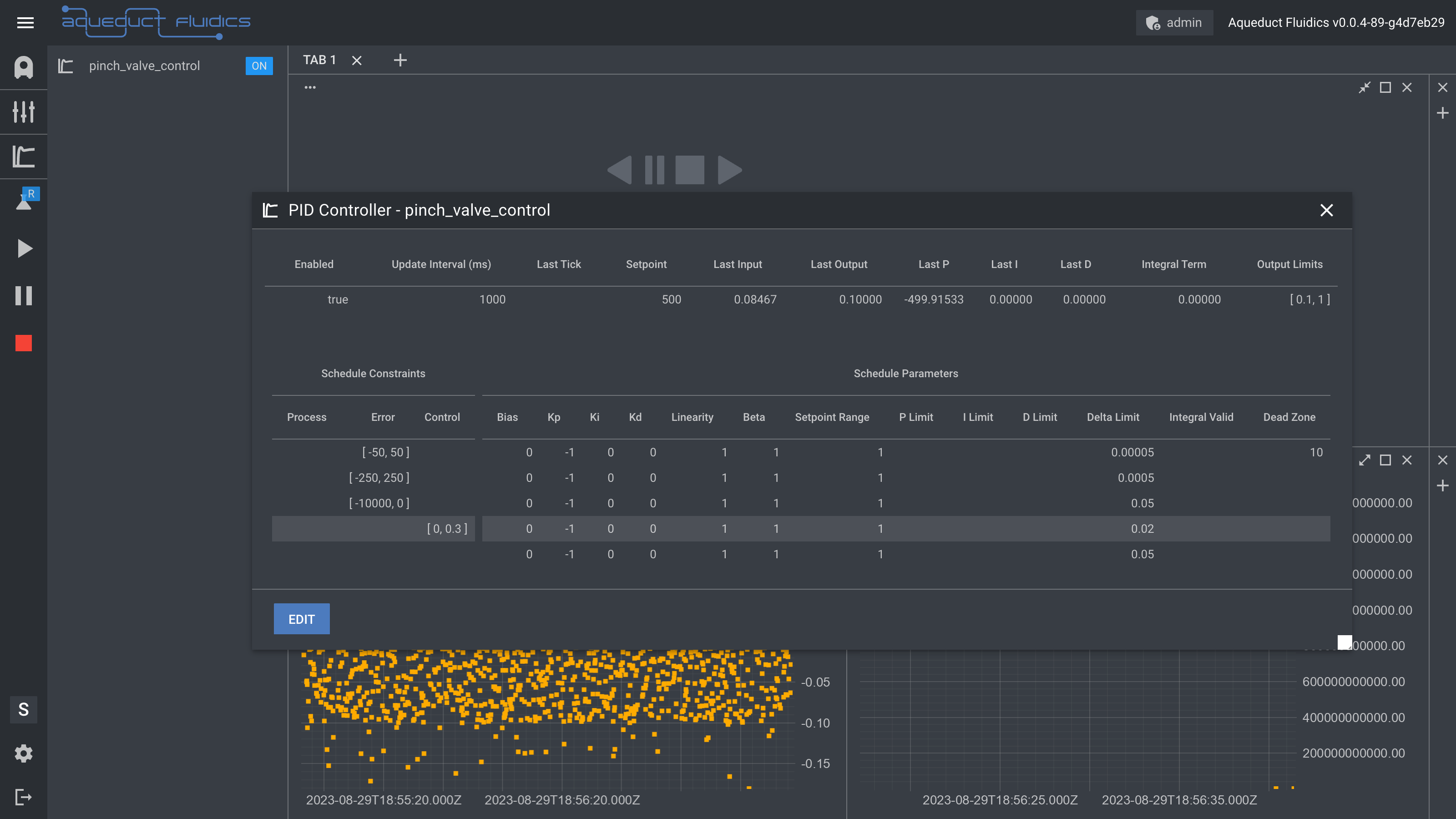
Schedule-based Parameter Selection:
- Dynamically selects control parameters based on Process Value, Control Output, or Error.
- Useful for managing non-linear processes with different operating regions.
- Example: Pinch valve control in the pinch valve application.
-
Contribution Limiting for P, I, or D Terms:
- Allows limiting the contribution of individual terms to the Control Output.
- Prevents issues like integral windup and excessive derivative action.
- Enhances control stability and performance.
-
Process Value-based Derivative Calculation:
- Utilizes the derivative of the Process Value instead of the derivative of the Error.
- Helps avoid undesirable control actions like derivative kick.
- Improves response to changes in the process variable.
-
Limiting of Maximum \(\Delta CO\) (Change in Control Output):
- Restricts the maximum change in control output between consecutive updates.
- Prevents abrupt and unwanted fluctuations in the control output.
- Example: Capping the maximum change in pinch valve position at 5%.
-
Dead Zone Functionality:
- Configurable band around the setpoint where the controller remains inactive.
- Prevents continuous adjustments within a specific range of the setpoint.
- Example: No adjustments to pump rate when pH is within 0.01 of the setpoint.
-
Control Output Limiting:
- Sets a boundary for the total process control output within a defined range.
- Ensures the control action remains within safe and effective limits.
- Example: Imposing a maximum rate on a peristaltic pump of 5 mL/min.
Overview of PID Control
Proportional-Integral-Derivative (PID) control is a widely used feedback control mechanism that strives to maintain a desired system state by adjusting a control output based on the difference between a setpoint and a measured process value. The Aqueduct PID Controller API provides a toolset for implementing PID control in various applications, offering efficient management of control loops.
Key Components of PID Control
-
Proportional (P) Term: The proportional term produces an output proportional to the current error (difference between setpoint and process value). It acts to bring the system closer to the desired state. Adjusting the proportional gain (kp) amplifies or dampens the response to error, influencing the control output's speed and stability.
-
Integral (I) Term: The integral term considers the cumulative effect of past errors and generates an output to eliminate the accumulated error over time. This is particularly useful in handling steady-state errors and eliminating biases. The integral gain (ki) controls the rate at which the accumulated error is corrected.
-
Derivative (D) Term: The derivative term anticipates the future error trend by evaluating the rate of error change. It provides a damping effect, preventing overshooting and oscillations. The derivative gain (kd) influences the system's responsiveness to rapid changes in error.