Simulated Model - Aqueduct Documentation

Simulating a TFF Process Using the Aqueduct Application

The Aqueduct application provides simulation capabilities that allow for the modeling of a TFF process. This guide outlines how to model the process using mathematical equations and Python code. It covers calculations for retentate, feed, and permeate pressures, as well as rates-of-change for balances that measure buffer, feed, and permeate product volumes.

The approach outlined in this guide is not limited to TFF systems; it can be readily adapted for other in-line and batch bioprocess applications.

Process Variables
- Independent Variables
- Dependent Variables
Calculating Pinch Valve \( \text{Cv} \)
Calculating Retentate Pressure
Calculating Feed Pressure
Calculating Permeate Pressure
Calculating Balance Rates-of-Change
Appendix
- Model in Action
- Full Code

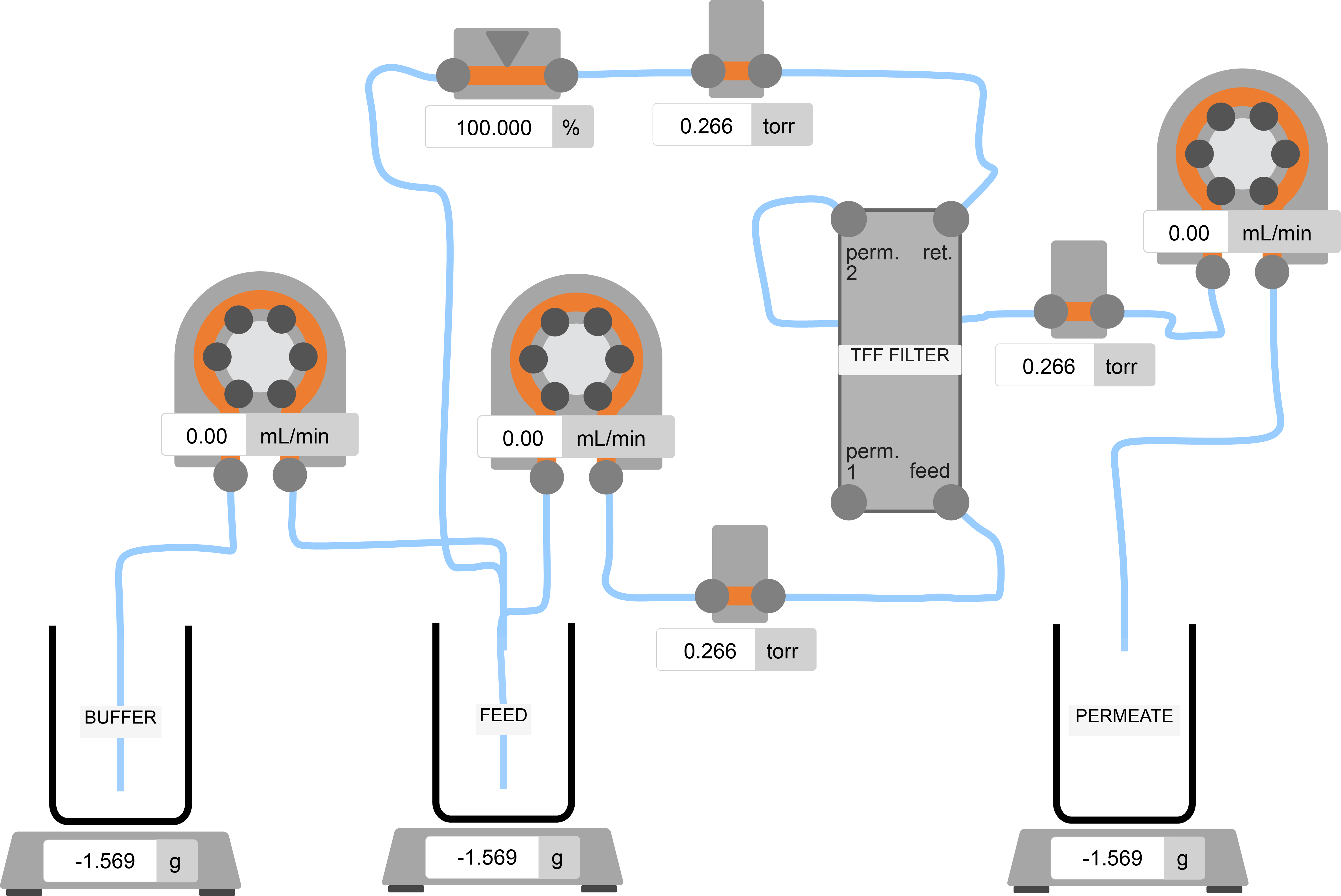
opentff

Independent Process Variables

The model takes the following independent variables as input parameters:

Feed Pump Rate - Flow rate of the feed pump (e.g., mL/min).
Buffer Pump Rate - Flow rate of the buffer pump (e.g., mL/min).
Permeate Pump Rate - Flow rate of the permeate pump (e.g., mL/min).
Pinch Valve Position - Position of the pinch valve, converted into a Valve Flow Coefficient (Cv) value.

The independent process variables are set by user interactions (either through the UI or a an Aqueduct Recipe).

Dependent Variables

Using the independent process variables, the simulation calculates the following dependent variables:

Feed Pressure - Pressure at the feed side of the filter.
Retentate Pressure - Pressure on the retentate side of the filter.
Permeate Pressure - Pressure on the permeate side of the filter.
Weight on Buffer Balance - Weight rate-of-change on the buffer balance.
Weight on feed Balance - Weight rate-of-change on the feed balance.
Weight on Permeate Balance - Weight rate-of-change on the permeate balance.

graph TD

A[Start] --> B[Calculate Pinch Valve Cv];
B --> C[Calculate Retentate Pressure<br>using Pinch Valve Cv and Feed Rate];
C --> D[Calculate Feed Pressure<br>using Permeate Pressure, Filter Cv, and Feed Rate];
D --> E[Calculate Permeate Pressure<br>using Feed and Retentate Pressure<br>and Permeate Flux];
E --> F[Calculate Mass Accumulation<br>on Feed, Buffer, and Permeate<br>Balances using Feed Rate,<br>Permeate Flux, and Buffer Pump Rate];
F --> G[End];

click B "#calculating-pinch-valve-textcv" _blank
click C "#calculating-retentate-pressure" _blank
click D "#calculating-feed-pressure" _blank
click E "#calculating-permeate-pressure" _blank
click F "#calculate-balance-rates-of-change" _blank

Calculating Pinch Valve \(\text{Cv}\)

We start the \(\text{Cv}\) calculation by estimating the percentage of occluded area in the cross-section of a tube based on its change in height (\( \Delta h \)).

The underlying mathematics are derived from this paper. The occlusion value scales between 0 and 1, where 1 indicates maximum occlusion (tube completely pinched), and 0 indicates no occlusion (tube retains original shape).

@staticmethod
def occluded_area_pct(delta_h: float) -> float:
    """
    Calculate the percentage change in cross-sectional area of a 
    tube when it's squeezed, based on the change in height.

    See: https://www.hindawi.com/journals/mpe/2015/547492/

    Parameters:
    delta_h (float): The change in height due to the squeeze as a 
    fraction of the original height (ranging from 0 to 1).

    Returns:
    float: The percentage change in the new cross-sectional area, scaled between 0 and 1. 
        1 indicates maximum occlusion (tube completely flat), 
        0 indicates no occlusion (tube retains original shape).
    """
    x = max(.5 - delta_h, 0)
    oc = math.pi * x * (math.sqrt(-20 * x**2 + 12 * x + 3) / 6 - (2 * x / 3) + 0.5)
    oc = min(-1 * (oc-0.7853981633974483), 1)
    return oc

The occluded area vs. \( \Delta h \) relationship is illustrated in the following plot:

opentff

After calculating the percentage of occluded area, we scale the original tube cross sectional area using the inner diameter in mm to \(\text{Cv}\) value using the functions:

@staticmethod
def cv_from_area_mm(area_mm: float) -> float:
    # Convert the area from mm^2 to m^2
    area_m = area_mm * 1e-6
    
    # Calculate the diameter from the area
    diameter_m = math.sqrt((4 * area_m) / math.pi)

    # Calculate Cv using the given formula
    Cv = (((diameter_m) ** 2) * 0.61) * 46250.9

    return Cv

@staticmethod
def calc_pv_cv(position: float) -> float:
    """
    Calculate the Cv of the pinch valve.

    :param PV: Pinch valve position.
    :type PV: float

    :return: Cv of the pinch valve.
    :rtype: float
    """
    response_zone = 0.35

    if position < response_zone:
        area = (math.pi * (5 / 2)**2)  * \
          (1 - PressureModel.occluded_area_pct((response_zone - position)/response_zone))
        return PressureModel.cv_from_area_mm(area_mm=area)
    else:
        return 100

Pinch Valve \(\text{Cv}\) Calculation

Next, we calculate the \(\text{Cv}\) value using the following steps:

Check Valve Position: If the valve's open position is below the response_zone threshold (0.35), we proceed to calculate the Cv by adjusting the cross-sectional area of the tube. This simulates the large range of the pinch valve position that does not have any affect on the tubing restriction area and will help us to develop control algorithms later.
Calculate Occluded Area: We use the occluded_area_pct method to find the percentage of the tube's area that is occluded or squeezed due to the valve's position.
Scale Original Tube Area: The original cross-sectional area of the tube (calculated using the tube's inner diameter of 5 mm) is then scaled by (1 - occluded_area_pct) to find the actual cross-sectional area when the valve is at the given position.
Calculate Cv: With the actual area in hand, we proceed to calculate the Cv value using the cv_from_area_mm method.

The following plot illustrates the relationship between \(\text{Cv}\) and the pinch valve position (in percent open, from 0 to 1).

opentff

Calculating Retentate Pressure

After we've calculated the flow coefficent \(\text{Cv}\) of the pinch valve based on its position, we can calculate the retentate pressure.

Obtain Feed Pump Rate: We use the (independent) feed pump rate process variable to set the mass flow through the restriction, \(Q\).
Apply Flow-Pinch Valve Relationship: The pressure drop across a restriction is related to the flow rate \(Q\) and the \(\text{Cv}\) of the restriction by the equation:

\[ \Delta P_{\text{psi}} = \left( \frac{Q}{0.865 \times \text{Cv}} \right)^2 \times 14.5038 \]

Here, \(\Delta P\) is the pressure drop across the valve, \(Q\) is the mass flow rate in \(\frac{m^3}{hr}\), and \(\text{Cv}\) is the flow coefficient of the restriction.

In Python, the calc_delta_p_psi method is used to perform the calculation:

@staticmethod
def calc_delta_p_psi(mass_flow_rate_ml_min: float, cv: float) -> float:
    """
    Calculate the pressure drop between through a restriction
    using the metric equivalent flow factor (Kv) equation:

    Kv = Q * sqrt(SG / ΔP)

    Where:
    Kv : Flow factor (m^3/h)
    Q : Flowrate (m^3/h)
    SG : Specific gravity of the fluid (for water = 1)
    ΔP : Differential pressure across the device (bar)

    Kv can be calculated from Cv (Flow Coefficient) using the equation:
    Kv = 0.865 * Cv

    :param mass_flow_rate_ml_min: Flowrate.
    :type mass_flow_rate_ml_min: float

    :param cv: Flow Coefficient.
    :type cv: float

    :return: Pressure drop (psi).
    :rtype: float
    """
    try:
        kv = 0.865 * cv
        # Convert mL/min to m^3/h
        delta_p_bar = 1 / (kv / (mass_flow_rate_ml_min / 60.0)) ** 2
        delta_p_psi = delta_p_bar * 14.5038  # Convert bar to psi
        return delta_p_psi
    except ZeroDivisionError:
        return 0

Calculate Retentate Pressure: Now that we have \( \Delta P \), we can calculate the retentate pressure using the following equation:

\[ P_{\text{Retentate}} = P_{\text{atm}} + \Delta P \]

where \( P_{\text{atm}} \) is atmospheric pressure. \( \Delta P \) is the pressure drop across the pinch valve, which we calculated earlier. Since we're interested in gage pressure (pressure above atomospheric pressure), we can neglect \( P_{\text{atm}} \) and:

\[ P_{\text{Retentate}} = \Delta P \]

The relationship between feed rate (in mL/min), pinch valve position (from 0 to 1, 1 being fully open), and the retentate pressure is illustrated in the following plot:

opentff

Calculating Feed Pressure

Once we know the retentate pressure, we can calculate the feed pressure using the \(\text{Cv}\) value for the pass-through stream of the TFF filter and the mass flow rate, as set by the feed pump.

The \(\text{Cv}\) value represents the flow coefficient of the pass-through stream's filter section.

The equation for calculating the feed pressure \( (P_{\text{feed}}) \) is:

\[ P_{\text{feed}} = P_{\text{retentate}} + \Delta P_{\text{pass-through}} \]

Where \( \Delta P_{\text{pass-through}} \) is the pressure drop across the pass-through leg of the TFF filter. This pressure drop can be calculated using the calc_delta_p_psi() function, which takes in the mass flow rate and \(\text{Cv}\) value as parameters and returns \( \Delta P \) in psi.

Here is the relevant Python code snippet to compute \( P_{\text{feed}} \):

def calc_feed_pressure_psi(
    self, 
    feed_rate_ml_min: float, 
    retentate_pressure_psi: float
  ) -> float:
    """
    Calculate the feed pressure.

    :param feed_rate_ml_min: Flow rate in the pass-through leg of the TFF filter (ml/min).
    :type feed_rate_ml_min: float

    :param retentate_pressure_psi: Retentate pressure (psi).
    :type retentate_pressure_psi: float

    :return: feed pressure (psi).
    :rtype: float
    """
    return retentate_pressure_psi + \
      self.calc_delta_p_psi(feed_rate_ml_min, PressureModel.filter_cv_retentate)

Experimental measurements yield \(\text{Cv}_{filter} \approx 0.86\) for our Pelicon filter.

Calculating Permeate Pressure

Once we have the retentate and feed pressures, we can calculate the permeate pressure.

The formula for calculating the permeate pressure is based on the work by Juang et al., who used a resistance-in-series model to estimate the permeate flux in TFF systems.

The formula for the permeate flux \( Q_{\text{permeate}} \) is given by:

\[ Q_{\text{permeate}} = \frac{TMP}{\mu R_m} \]

where \( TMP \) is the transmembrane pressure, \( \mu \) is the fluid viscosity, and \( R_m \) is the total resistance of the membrane. We simplify the model by taking \(\mu R_m \) to be constant (experimental measurements yield \(\mu R_m \approx 0.8 \)).

The Python code snippet to compute \( Q_{\text{permeate}} \):

def calc_permeate_pressure(
    feed_pressure_psi: float,
    retentate_pressure_psi: float,
    permeate_rate_ml_min: float
) -> float:
    """
    Calculate the permeate pressure.

    :param feed_pressure_psi: feed pressure (psi).
    :type feed_pressure_psi: float

    :param retentate_pressure_psi: Retentate pressure (psi).
    :type retentate_pressure_psi: float

    :param permeate_rate_ml_min: Permeate flow rate (ml/min).
    :type permeate_rate_ml_min: float

    :return: Permeate pressure (psi).
    :rtype: float
    """
    try:
        avg_psi = (feed_pressure_psi + retentate_pressure_psi) / 2
        return avg_psi - permeate_rate_ml_min * .8
    except ZeroDivisionError:
        return 0

The relationship between permeate rate (in mL/min), average input pressure \( \frac{ P_{\text{feed}} + P_{\text{retentate}} }{2} \) (in psi), and the permeate pressure is illustrated in the following plot:

opentff

Calulcate Balance Rates-of-Change

Finally, we update the simulated rates of change on the buffer, feed, and permeate balances using mass conservation.

Buffer Balance

If a buffer pump is present, the flow rate (ml/min) of the buffer pump is taken into consideration.
The ROC (balance_rocs) for the buffer balance is determined by taking the negative of the flow rate of the buffer pump (buffer_pump_ml_min), simulating mass removal.
Optionally, this ROC is adjusted to simulate a deviation (buffer_scale_error_pct) that may exist between the nominal flow rate of the pump and the actual mass removal rate from the buffer scale. The error term is added to 1 and then multiplied by the negative flow rate of the buffer pump.

Permeate Balance

The ROC for the permeate balance is calculated based on the flow rate (ml/min) of the permeate pump (permeate_pump_ml_min).
Optionally, this ROC is adjusted to simulate a deviation (retentate_scale_error_pct) that may exist between the nominal flow rate of the pump and the actual mass addition to the permeate scale. The error term is added to 1 and then multiplied by the flow rate of the permeate pump.

Feed Balance

The rate of change for the feed balance is calculated by summing the ROCs of the buffer and permeate balances.
The sum is then negated to give the final ROC for the feed balance.

After all the ROCs are calculated, they are converted from ml/min to ml/s by dividing them by 60. These new rates are then set as the simulated rates of change for the balances in the system (self.balances.set_sim_rates_of_change(balance_rocs)).

Appendix

Model in Action

The following video snippet shows how the simulated pressure and weight values are bound to the independent process values. Modifying the pump's rates and changing the pinch valve position drive responses in the feed, retentate, and permeate pressures and the rates-of-change on the balances.

Full Code

To run the model, first install the application and then load the TFF - System setup (link here) in the application. Separately, execute the command:

python examples/models/tff.py -r 0

to run the model as an unregistered recipe.

Filename: examples/models/tff.py

import math
import time
import typing

from aqueduct.core.aq import Aqueduct
from aqueduct.core.aq import InitParams
from aqueduct.core.units import PressureUnits
from aqueduct.devices.balance import Balance
from aqueduct.devices.pressure.transducer import PressureTransducer
from aqueduct.devices.pump.peristaltic import PeristalticPump
from aqueduct.devices.valve.pinch import PinchValve


class PressureModel:
    """
    This simple model estimates the pressures:
        - feed (between feed pump and TFF feed input)
        - retentate (between TFF retentate outlet and PV)
        - permeate (between TFF permeate outlet and permeate pump)
    using the current pump flow rates and pinch valve position
    as input parameters.

    Procedure:
        1. model Cv of the pass through (feed-retentate) leg of the TFF filter using
           P1 - P2 for known flow rates
        2. model Cv of the pinch valve using a non-linear expression that decreases
           as ~(% open)**-2 with an onset pct open of 0.3 (30%)
        3. calculate retentate pressure assuming atmospheric output pressure and using Cv pinch valve
        4. calculate feed pressure using retentate pressure and Cv TFF pass through
        5. calculate permeate pressure using the expression for TMP

    :ivar filtration_start_time: Start time of the filtration process.
    :vartype filtration_start_time: float

    :ivar filter_cv_retentate: Cv value of the retentate leg of the TFF filter.
    :vartype filter_cv_retentate: float
    """

    filter_cv_retentate: float = 0.87

    @staticmethod
    def cv_from_diameter_mm(diameter: float) -> float:
        Cv = (((diameter / 1000) ** 2) * 0.61) * 46250.9
        return Cv

    @staticmethod
    def cv_from_area_mm(area_mm: float) -> float:
        # Convert the area from mm^2 to m^2
        area_m = area_mm * 1e-6

        # Calculate the diameter from the area
        diameter_m = math.sqrt((4 * area_m) / math.pi)

        # Calculate Cv using the given formula
        Cv = (((diameter_m) ** 2) * 0.61) * 46250.9

        return Cv

    @staticmethod
    def occluded_area_pct(delta_h: float) -> float:
        """
        Calculate the percentage change in cross-sectional area of a tube when it's squeezed, based on the change in height.

        See: https://www.hindawi.com/journals/mpe/2015/547492/

        Parameters:
        delta_h (float): The change in height due to the squeeze as a fraction of the original height (ranging from 0 to 1).

        Returns:
        float: The percentage change in the new cross-sectional area, scaled between 0 and 1.
            1 indicates maximum occlusion (tube completely flat),
            0 indicates no occlusion (tube retains original shape).
        """
        x = max(0.5 - delta_h, 0)
        oc = (
            math.pi * x * (math.sqrt(-20 * x**2 + 12 * x + 3) / 6 - (2 * x / 3) + 0.5)
        )
        oc = min(-1 * (oc - 0.7853981633974483), 1)
        return oc

    @staticmethod
    def calc_pv_cv(position: float) -> float:
        """
        Calculate the Cv of the pinch valve.

        :param PV: Pinch valve position.
        :type PV: float

        :return: Cv of the pinch valve.
        :rtype: float
        """
        response_zone = 0.35

        if position < response_zone:
            area = (math.pi * (5 / 2) ** 2) * (
                1
                - PressureModel.occluded_area_pct(
                    (response_zone - position) / response_zone
                )
            )
            return PressureModel.cv_from_area_mm(area_mm=area)
        else:
            return 100

    @staticmethod
    def calc_delta_p_psi(mass_flow_rate_ml_min: float, cv: float) -> float:
        """
        Calculate the pressure drop between through a restriction
        using the metric equivalent flow factor (Kv) equation:

        Kv = Q * sqrt(SG / ΔP)

        Where:
        Kv : Flow factor (m^3/h)
        Q : Flowrate (m^3/h)
        SG : Specific gravity of the fluid (for water = 1)
        ΔP : Differential pressure across the device (bar)

        Kv can be calculated from Cv (Flow Coefficient) using the equation:
        Kv = 0.865 * Cv

        :param mass_flow_rate_ml_min: Flowrate.
        :type mass_flow_rate_ml_min: float

        :param cv: Flow Coefficient.
        :type cv: float

        :return: Pressure drop (psi).
        :rtype: float
        """
        try:
            kv = 0.865 * cv
            # Convert mL/min to m^3/h
            delta_p_bar = 1 / (kv / (mass_flow_rate_ml_min / 60.0)) ** 2
            delta_p_psi = delta_p_bar * 14.5038  # Convert bar to psi
            return delta_p_psi
        except ZeroDivisionError:
            return 0

    @staticmethod
    def calc_delta_p_rententate_psi(
        feed_rate_ml_min: float, pinch_valve_position: float
    ) -> float:
        """
        Calculate the pressure drop between retentate and atmospheric output
        using the metric equivalent flow factor (Kv) equation:

        :param feed_rate_ml_min: Flow rate in the pass-through leg of the TFF filter.
        :type feed_rate_ml_min: float

        :param pinch_valve_position: Pinch valve position.
        :type pinch_valve_position: float

        :return: Pressure drop between retentate and atmospheric outlet.
        :rtype: float
        """
        cv = PressureModel.calc_pv_cv(pinch_valve_position)
        return PressureModel.calc_delta_p_psi(feed_rate_ml_min, cv)

    def calc_feed_pressure_psi(
        self, feed_rate_ml_min: float, retentate_pressure_psi: float
    ) -> float:
        """
        Calculate the feed pressure.

        :param feed_rate_ml_min: Flow rate in the pass-through leg of the TFF filter (ml/min).
        :type feed_rate_ml_min: float

        :param retentate_pressure_psi: Retentate pressure (psi).
        :type P2: float

        :return: P1 pressure.
        :rtype: float
        """
        return retentate_pressure_psi + self.calc_delta_p_psi(
            feed_rate_ml_min, PressureModel.filter_cv_retentate
        )

    @staticmethod
    def calc_permeate_pressure(
        feed_pressure_psi: float,
        retentate_pressure_psi: float,
        permeate_rate_ml_min: float,
    ) -> float:
        """
        Calculate the permeate pressure pressure.

        https://aiche.onlinelibrary.wiley.com/doi/epdf/10.1002/btpr.3084

        :param feed_pressure_psi: Feed pressure.
        :type feed_pressure_psi: float

        :param retentate_pressure_psi: Retentate pressure.
        :type retentate_pressure_psi: float

        :param permeate_rate_ml_min: Permeate flow rate.
        :type permeate_rate_ml_min: float

        :return: Premeate pressure (psi).
        :rtype: float
        """
        try:
            avg_psi = (feed_pressure_psi + retentate_pressure_psi) / 2
            return avg_psi - permeate_rate_ml_min * 0.8
        except ZeroDivisionError:
            return 0

    def calc_pressures(
        self,
        feed_pump_ml_min: float,
        permeate_pump_ml_min: float,
        pinch_valve_position: float,
    ):
        """
        Calculate and update the pressures using the model equations.
        """
        retentate_pressure_psi = PressureModel.calc_delta_p_rententate_psi(
            feed_pump_ml_min, pinch_valve_position
        )

        feed_pressure_psi = self.calc_feed_pressure_psi(
            feed_pump_ml_min, retentate_pressure_psi
        )

        permeate_pressure_psi = PressureModel.calc_permeate_pressure(
            feed_pressure_psi, retentate_pressure_psi, permeate_pump_ml_min
        )

        feed_pressure, retentate_pressure, permeate_pressure = (
            min(feed_pressure_psi, 50),
            min(retentate_pressure_psi, 50),
            min(permeate_pressure_psi, 50),
        )

        return (feed_pressure, retentate_pressure, permeate_pressure)


class Model:
    """
    This class manages the simulation model for a Tangential Flow Filtration (TFF) system.
    It integrates various components such as feed, permeate, and buffer pumps, balances for
    fluid levels, pressure transducers, and a pinch valve. It also contains methods to compute
    derived values for these components based on real-time simulation parameters.

    Attributes:
        buffer_balance_index (int): Index for the buffer balance.
        feed_balance_index (int): Index for the feed balance.
        permeate_balance_index (int): Index for the permeate balance.

        feed_transducer_index (int): Index for the feed pressure transducer.
        permeate_transducer_index (int): Index for the permeate pressure transducer.
        retentate_transducer_index (int): Index for the retentate pressure transducer.

        buffer_scale_error_pct (float): Error percentage for the buffer scale.
        retentate_scale_error_pct (float): Error percentage for the retentate scale.

        pressure_model (PressureModel): An instance of PressureModel to handle pressure calculations.
    """

    buffer_balance_index: int = 1
    feed_balance_index: int = 0
    permeate_balance_index: int = 2

    feed_transducer_index: int = 0
    permeate_transducer_index: int = 2
    retentate_transducer_index: int = 1

    buffer_scale_error_pct: float = 0.00001
    retentate_scale_error_pct: float = 0.00001

    pressure_model: PressureModel

    def __init__(
        self,
        feed_pump: PeristalticPump,
        permeate_pump: PeristalticPump,
        buffer_pump: typing.Union[PeristalticPump, None],
        balances: Balance,
        transducers: PressureTransducer,
        pinch_valve: PinchValve,
    ):
        """
        Initialize the Model with given pumps, balances, transducers, and pinch valve.

        Args:
            feed_pump (PeristalticPump): The feed pump object.
            permeate_pump (PeristalticPump): The permeate pump object.
            buffer_pump (PeristalticPump or None): The buffer pump object or None.
            balances (Balance): The balance object to manage fluid balances.
            transducers (PressureTransducer): The pressure transducers.
            pinch_valve (PinchValve): The pinch valve object.
        """
        self.feed_pump = feed_pump
        self.permeate_pump = permeate_pump
        self.buffer_pump = buffer_pump
        self.balances = balances
        self.transducers = transducers
        self.pinch_valve = pinch_valve

        self.pressure_model = PressureModel()

    def calculate(self):
        """
        Calculate the derived values for all pressure transducers and balances.
        """
        balance_rocs = [0, 0, 0, 0]

        buffer_pump_ml_min = 0

        # if BUFFER PUMP is present, use this to drive sim value balance
        if isinstance(self.buffer_pump, PeristalticPump):
            buffer_pump_ml_min = self.buffer_pump.live[0].ml_min
            balance_rocs[self.buffer_balance_index] = (-1 * buffer_pump_ml_min) * (
                1.0 + self.buffer_scale_error_pct
            )

        feed_pump_ml_min = self.feed_pump.live[0].ml_min
        permeate_pump_ml_min = self.permeate_pump.live[0].ml_min
        pv_position = self.pinch_valve.live[0].pct_open

        balance_rocs[self.permeate_balance_index] = permeate_pump_ml_min * (
            1.0 + self.retentate_scale_error_pct
        )

        balance_rocs[self.feed_balance_index] = -1 * (
            balance_rocs[self.buffer_balance_index]
            + balance_rocs[self.permeate_balance_index]
        )

        # mL/min to mL/s
        balance_rocs = [r / 60.0 for r in balance_rocs]

        self.balances.set_sim_rates_of_change(balance_rocs)

        (
            feed_pressure,
            retentate_pressure,
            permeate_pressure,
        ) = self.pressure_model.calc_pressures(
            feed_pump_ml_min, permeate_pump_ml_min, pv_position
        )

        self.transducers.set_sim_values(
            [feed_pressure, retentate_pressure, permeate_pressure], PressureUnits.PSI
        )


if __name__ == "__main__":

    # Parse the initialization parameters from the command line
    params = InitParams.parse()

    # Initialize the Aqueduct instance with the provided parameters
    aq = Aqueduct(
        params.user_id,
        params.ip_address,
        params.port,
        register_process=params.register_process,
    )

    # Perform system initialization if specified
    aq.initialize(params.init)

    # Set a delay between sending commands to the pump
    aq.set_command_delay(0.05)

    # Define names for devices
    FEED_PUMP_NAME = "MFPP000001"
    BUFFER_PUMP_NAME = "MFPP000002"
    PERMEATE_PUMP_NAME = "MFPP000003"
    BALANCES_NAME = "OHSA000001"
    TRANSDUCERS_NAME = "SCIP000001"
    PINCH_VALVE_NAME = "PV000001"

    # Retrieve device instances
    feed_pump: PeristalticPump = aq.devices.get(FEED_PUMP_NAME)
    permeate_pump: PeristalticPump = aq.devices.get(PERMEATE_PUMP_NAME)
    buffer_pump: PeristalticPump = aq.devices.get(BUFFER_PUMP_NAME)
    balances: Balance = aq.devices.get(BALANCES_NAME)
    transducers: PressureTransducer = aq.devices.get(TRANSDUCERS_NAME)
    pinch_valve: PinchValve = aq.devices.get(PINCH_VALVE_NAME)

    balances.set_sim_noise([0.0001, 0.0005, 0.0001])
    transducers.set_sim_noise([0.0001, 0.0001, 0.0001])

    # Create an instance of the PressureModel
    model = Model(
        feed_pump, permeate_pump, buffer_pump, balances, transducers, pinch_valve
    )

    # Continuous pressure calculation loop
    while True:
        model.calculate()
        time.sleep(0.1)